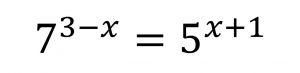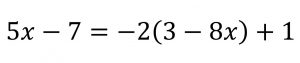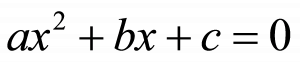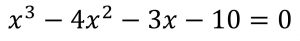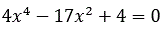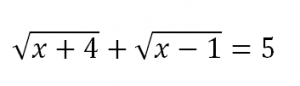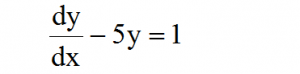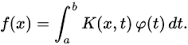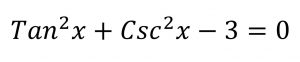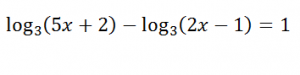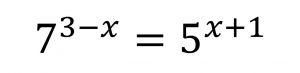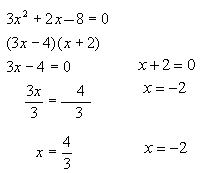En el mundo de las matemáticas existen multitud de
ecuaciones que nos ayudan a resolver toda clase de problemas. Por ello, es necesario conocer todos los tipos de ecuaciones según su formas y características. Gracias a esta clasificación de ecuaciones podremos identificarlas cuando nos encontremos con ellas.
Clasificación de ecuaciones
Aquí podrás encontrar los tipos de ecuaciones matemáticas que existen, clasificados según su naturaleza. También encontrarás los tipos de ecuaciones con ejemplos, para que te ayuden a comprender mejor sus características.
Ecuaciones algebraicas o polinómicas
Las funciones algebraicas o funciones polinómicas son las ecuaciones que introducen
polinomios dentro de sus expresiones. Podemos encontrar diferentes tipos de funciones polinómicas según el grado de la ecuación. El grado de la ecuación se determina por el mayor exponente.
Ecuaciones lineales o de primer grado
Las
ecuaciones de primer grado o ecuaciones lineales, se definen como las expresiones con una o más incógnitas elevadas a la primera potencia. Se denominan lineales porque representan una línea en el eje cartesiano. Aprende a encontrar la solución de estas ecuaciones con los ejercicios de ecuaciones de primer grado.
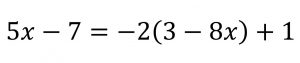
Ecuaciones cuadráticas o de segundo grado
La
ecuaciones de segundo grado, también llamadas ecuaciones cuadráticas, son aquellas cuyo mayor grado es 2. Puedes aprender a resolver ecuaciones de este tipo con los ejercicios de ecuaciones de segundo grado.
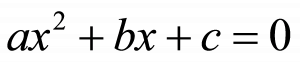
Ecuaciones de tercer grado
Se denominan
ecuaciones de tercer grado todas las ecuaciones cuyo mayor grado es 3. Sucesivamente, según el grado que posean las ecuaciones se consideran 'ecuaciones de grado n' donde n es el mayor exponente de la ecuación. De forma que si en una ecuación n=7, se denomina ecuación de grado 7.
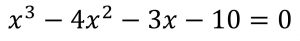
Ecuaciones bicuadradas
La
ecuaciones bicuadradas son un tipo de ecuación de cuarto grado que no posee términos impares. La fórmula de las ecuaciones bicuadradas es: ax4+bx2+c=0
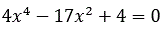
Ecuaciones irracionales
Las
ecuaciones irracionales también poseen el nombre de ecuaciones radicales. Estas ecuaciones se caracterizan por tener la incógnita dentro de un radical y existe un procedimiento para resolverlas de forma correcta.
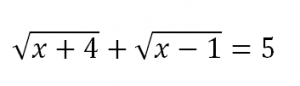
Ecuaciones no algebraicas
Este tipo de ecuaciones vienen determinadas por otros tipos de operaciones que no se corresponden con el
álgebra lineal.
Ecuaciones diferenciales
Las ecuaciones diferenciales, son aquellas que vienen determinadas por las derivadas de una o más funciones. Según el número de variables independientes, pueden ser ecuaciones diferenciales ordinarias, o ecuaciones derivadas parciales.
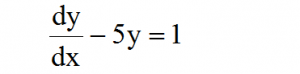
Ecuaciones integrales
En las ecuaciones integrales, vemos que la función incógnita se encuentra dentro de una operación integral. Este tipo de ecuaciones se leen como 'integral de f(x)' o 'diferencial de x'. Las ecuaciones integrales y diferencialesestán estrechamente relacionadas, y se pueden utilizar las dos para plantear algunos problemas matemáticos.
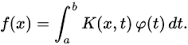
Ecuaciones trigonométricas
Las
ecuaciones trigonométricas son las ecuaciones cuya incógnita se encuentran afectada por una función trigonométrica. Podemos encontrar resultados infinitos, debido a que estas funciones son periódicas.
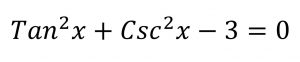
Ecuaciones logarítmicas
Llamamos
ecuaciones logarítmicas a aquellas ecuaciones, donde la incógnita se ve afectada por algún logaritmo. Para resolverlas debemos aplicar las diferentes propiedades que de los logaritmos.
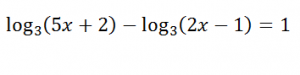
Ecuaciones exponenciales
La incógnita de las
ecuaciones potenciales se sitúa en el exponente de cada una de las potencias. Es posible que encontremos la incógnita en uno de los componentes de la ecuación, o en cada uno de los elementos que aparecen. Es muy importante conocer las
propiedades de las potencias para poder resolverlas.